ssk tech blog

自律移動ロボットの話を書きます

【論文】Google Cartographerの論文【ICRA2016】

Robot SLAM 論文 Cartographer

目次

はじめに

こんにちは．ササキ(@saitosasaki)です．
私は以前Google Cartographer(OSS中でおそらく一番性能の良いグラフベースSLAM）の論文を読んだことがあったので復習のため、(かつどこにも解説スライドや記事が上がってなさそうなので)、まとめをブログに挙げます。

Github
github.com 論文
Real-Time Loop Closure in 2D LIDAR SLAM

予備知識

下記の解説論文を読めば、Cartographerの基礎となるgraph-based slamのことがわかると思います。
移動ロボットの環境認識 —地図構築と自己位置推定 - J-Stage

論文

概要

  • 背景と課題
    LIDAR-SLAMは、間取り図を取得する効率的な方法である。 地図をリアルタイムで生成して可視化することで、オペレータはキャプチャデータの品質とカバレッジを評価できる。 携帯型キャプチャプラットフォームを構築するには、限られた計算リソースの下で動作する必要がある。
  • 提案手法
    本論文では、5 cmの解像度でリアルタイムマッピングとループクロージャを実現するアプローチを紹介する。 リアルタイムなループクロージャを達成するために、制約としてスキャン対サブマップの一致を計算するための分岐限定(branch-and-bound)法を使用する。
  • 実験
    確立された技術と競合することを示すために、提案手法と他のよく知られたアプローチと比較する。

スライド

今回のまとめはスライド形式にしてみました（というか結構前に自分が作ったのを修正しただけなのですが）。 speakerdeck.com

おわりに

スライドでまとめると、論文の直訳ではなく、自分の言葉で書く必要があるので、作るとより理解できてる気がします。発表するにはもうちょいスライドの内容を間引く必要がありますね。あともっとオリジナルの図を入れてわかりやくしたいですね。反省。
実験結果はオーソドックスで特筆することも無さ気なので書いてません。書いたほうがいいんですかね？
表現にいろいろ怒られそうなところはありますが、そのうち直します。…たぶん。

参考にした資料

論文と実装で変更された点

ほんとは別記事で書きたいのですが，とりあえずここに書いときます．

  • コスト関数
    実装におけるコスト関数．

google-cartographer.readthedocs.io

  • sparseという言葉の取り扱い
    論文だとグラフがspaerseなのを押し出していて，プログラムの初期のpose graphのプログラム名をsparse_pose_graph としていました．しかし，下記のissueで「pose graphはsparseなグラフなんだからsparseなんてつけるのはpoorだ」と言われて，作成者の方は最初こそ抵抗したものの，結局プログラムや関数名からsparseという言葉は無くなっています．

github.com

【論文】Unscented Kalman Filterのパラメータを逐次的にチューニングする論文を読む【2018】

論文 ベイズ

目次

はじめに

こんにちは．ササキ(@saitosasaki)です．
今回はある技術ブログのある記事で最後のほうに紹介されていた「アンセンテッドカルマンフィルタのパラメータをオートチューニングする」論文が気になったので読んでみました．

論文
[A Robust Adaptive Unscented Kalman Filter for Nonlinear Estimation with Uncertain Noise Covariance](https://www.researchgate.net/publication/323621421_A_Robust_Adaptive_Unscented_Kalman_Filter_for_Nonlinear_Estimation_with_Uncertain_Noise_Covariance}

UKF(Unscented Kalman Filter)について

　以下の東工大の山北先生の解説論文が6ページと短く、わかりやすくておすすめです。アンセンテッドの由来も書いてあって読み物としても面白いです。

UKF (Unscented Kalman Filter)って何?
ちなみにUnsecentedの由来は以下．

そこに込められている意味は手垢のついていない， まったく新しい発想に基づく手法であると いう意味らしい ，足立先生はこれらのことを考慮してUnscented を「無香料」と訳されている．

　「UKFの Unscented変換って結局なんなの？」という人は以下の記事を読むと良いと思います．
参考文献の片山先生の『非線形カルマンフィルタの基礎』を辿れば確認できるんですが，Gauss-Hermite求積由来です．
https://t.co/cpeAeeHV6D
上の記事消されてますね・・・悲しい．

カルマンフィルタの派生形についてのまとめ

論文を読む前に、有名なカルマンフィルタの派生形について整理しました。
基本『確率ロボティクス』のまとめです。ここには書いてないですけど，Ensemble Kalman Filter(EnKF)も有名ですね．
以前まとめたんですが、書く機会がなかったんでとりあえずここにまとめときます。

  • EKF(Extended Kalman Filter)はモデルを線形近似すれば、後はカルマンフィルタのアルゴリズムと同じ。

  • UKFは非線形なモデルのままで、事前分布の平均値の他に分布からシグマ点を数個とって、モデルに通した点から事後分布（正規分布）の平均値と分散を求める。
    分布からいくつかの点をサンプルするという意味ではUKFとPF(Particle Filter)は似ていて、違いはサンプルする点が決定論的かランダムか。

  • EKFとUKFの比較
    ・EKFの方がわずかにUKFより計算は速い.
    ・UKFの方が推定の正確性が上だが、非線形性や事前の状態の不確かさによってあまり差がないことも多い。
    ・UKFの場合微分が不要.
    ・UKFはハイパーパラメータが増えるので面倒.

論文

概要

  • 通常のUKFの問題点
    ユーザが事前に仮定した雑音分布と実際の非線形システムにおける実際のものとの間の不一致により、性能が劣化または発散する．
  • 提案手法
    本論文では、不確実な雑音の共分散による状態推定の精度とロバスト性を改善するためのRobust Adaptive UKF（RAUKF）を提案する。
  • アルゴリズム
    1.各タイムステップで、標準のUKFが最初に実行され、新しく取得された測定データを使用して状態推定値を取得する。
    2.次に、現在の雑音共分散を更新する必要があるかどうかを判断するためにオンラインで故障を検出する機構を使用する。
    　必要であれば、革新ベースの方法と残差ベースの方法を使用して、それぞれプロセスと測定の現在のノイズ共分散の推定値を計算する。 重み係数を利用することによって、フィルタは最後の雑音共分散行列を新しい雑音共分散行列としての推定と組み合わせる。
    3.最後に、新しい雑音共分散行列と以前の状態推定に従って状態推定を修正する。
  • 結果
    通常のUKFおよび他の適応UKFアルゴリズムと比較して、RAUKFは実際の雑音共分散に速く収束し、　　
    ロバスト性、精度、および不確かな雑音共分散による非線形推定のための計算に関してより良い性能を達成した。

Standard UKF(SUKF)による通常の状態推定

  • 動作モデル

x_k = f( x_{k-1}) + w_{k-1} (1)

  • 誤差共分散

P_{k}^{xx} = E((x_k - \hat{x}_{k \vert k})(x_k - \hat{x}_{k \vert k})^T)(2)
ここで、Eは平均を表す。

  • 観測モデル

z_k=h (x_k) + v_k(3)

f:id:ssk0109:20190502143349p:plain f:id:ssk0109:20190502143422p:plain
f:id:ssk0109:20190502143628p:plain

Robust Adaptive Unscented Kalman Filter(RAUKF)

  • 故障検出機構
    RAUKFは、現在の理論的推定値とシステムに障害が発生した場合の最後のデータとの重み付けの組み合わせに基づいて、ＱおよびＲを適応的に調整する。したがって、雑音共分散行列を修正する必要があるかどうかを判断するには、障害検出メカニズムを採用する必要がある。
    本論文で採用されている障害検出メカニズムは、研究 [19]で使用されているものと類似している。

\phi_k =\mu_{k}^{T} (\overline{P}_{k \vert k-1}^{zz})^{-1} \mu_k(17)

kはs自由度のχ2分布をもち、sはµkの次元である。 1-σの信頼性レベルを有する故障を検出したいと仮定する。ここで、σは選択されたパラメータである。 それから、

P(\phi_k > \xi^{2}_{\sigma、s} )= \sigma (18)

のように、ϕkの\xi^{2}_{\sigma、s}分布によって決定される閾値\xi^{2}_{\sigma、s}がある。 したがって、予め選択されたσの値を使用して、システム障害が1-σの信頼性レベルで検出され得るように、式(18)から対応する障害検出の閾値\chi^{2}_{\sigma、s}を定義する。

  • プロセスノイズQのAdaptive Adjustment
    イノベーションµkは、新しい測定値の結果としてフィルタに利用可能な追加情報を表す。 したがって、µkはフィルタ適応に最も関連のある情報と考えられ、雑音共分散を推定するために使用できる[23]。 式(1)によれば、プロセスノイズは、w_{k-1} = x_k - f(x_{k-1})として表すことができる。 さらに、SUKFの方程式から、プロセスノイズは次のようになる。

f:id:ssk0109:20190503105909p:plain

上記の導出で使用される線形化による２つの近似には、\overline{ｘ}_{k \vert k-1}\approx f(\hat{ｘ}_{k \vert k-1}) および\overline{z}_{k \vert k-1}\approx h(\hat{z}_{k \vert k-1})がある。 ここでは、時間k-1での平均の前方の展開は前方に展開したシグマ点から計算された平均によって近似される; それぞれ、平均値の観測値はシグマ点の観測値を介して計算された観測値の平均によって近似される。
　したがって、プロセスノイズ共分散行列Qk-1の推定は、次のように推定できる。

f:id:ssk0109:20190503105945p:plain

ここで、cov（∗）は共分散、 E（∗）は期待値である。
上記の式を実装するために、E(\mu_k \mu_k^{T}) は通常、windowing methodを使用して\mu_k \mu_k^{T}を時間平均することによって近似される。 moving window methodsを使用する代わりに（研究[15,19,23,29]のように）、本論文は、最後の雑音共分散値と現在の推定値とのバランスをとるために重み係数λを利用することによってＱを適応的に調整する。 重み係数λは、更新強度を保証するために下限λ０∈（０、１）で設定され、φｋが事前設定された閾値を超える場合、φｋの上昇につれて増加する。 したがって、システムプロセスノイズ共分散行列は次のように更新される。

Q_{k-1} = (1 - \lambda)Q_{k-1} + \lambda ( K_k \mu_k \mu_k^{T}K_k^{T} )(21)
\lambda = max(\lambda_0,(\phi_k - a \times \chi_{\sigma,s}^{2})/\phi_k)(22)

ここで、a（a> 0）は実際の環境に応じた調整パラメータであり、aが大きいほどデフォルトのλ0を使用する可能性が高いことを意味する。 特に、λ0とaの間のトレードオフが、共分散の更新が新しいイノベーションに対してどれほど敏感で あるかを決定する。

  • 観測ノイズRのAdaptive Adjustment
    時間ステップｋにおける測定雑音共分散行列Ｒはまた、以下のようにイノベーションに基づくアプローチによって推定できる。

f:id:ssk0109:20190503111005p:plain
ここで、

f:id:ssk0109:20190503111044p:plain

である。（導出プロセスについての詳細は、参考文献[30]を参照。）一般的に、R_{k}は共分散行列であるため、R_{k}は正定値であるべきである。しかしながら、式(23)からのその推定値\hat{R}_{k}は、２つの正定値行列を減算することによって得られるので、正定値行列であることを保証できない。それから、ノイズ共分散行列の主対角に負のパラメータがあると、適応フィルタは突然発散する[22]。正定行列\hat{R}_{k}を取得するには、残差ベースのアプローチを使用する。式(3)から、時間ステップｋにおける測定雑音は、v_k = x_k -h(x_k)として導出することができる。次に、タイムステップkにおける残差ベクトルは、

\varepsilon_k = z_k - h(\hat{x}_{k \vert k})(24)

で与えられる。
さらに、非特許文献２によれば、残差ベクトルεｋに基づく測定雑音共分散の推定は、次式で与えられる。

f:id:ssk0109:20190503110148p:plain

ここで、

f:id:ssk0109:20190503110126p:plain

前のセクションで使用された方法と同様に、Rkは以下のように下限値δ０∈(0,1)で設定された重み係数δを利用して更新される。

R_k = (1 - \delta)R_k + \delta ( \varepsilon_k \varepsilon_k^T+ \hat{S}_{k \vert k-1}^{zz} )(29)
\delta = max(\delta_0,(\phi_k - b \times \chi_{\sigma,s}^{2})/\phi_k)(30)

ここで、b(b>0)も実際の環境に依存する調整パラメータである。 ｂおよびδ0の選択は、ａおよびλ0の選択と同じである。

  • 状態推定の修正

f:id:ssk0109:20190502143015p:plain

  • 疑似コード

f:id:ssk0109:20190502140259p:plain:w400

シミュレーション結果

  • システムモデル

f:id:ssk0109:20190503114326p:plain

f:id:ssk0109:20190503114420p:plain

未知のノイズのある環境下でのシミュレーション結果

f:id:ssk0109:20190502140042p:plain:w400
f:id:ssk0109:20190502140127p:plain:w500

動的に変化するノイズのある環境下でのシミュレーション結果

プロセスノイズの共分散の条件
f:id:ssk0109:20190502135914p:plain
実験結果
f:id:ssk0109:20190502135508p:plain:w500
f:id:ssk0109:20190502135533p:plain:w500

感想

紹介されていたブログによると「パラメータをオートチューニングする論文」ということだったので、読む前はUKF固有のハイパーパラメータを実験したデータを基に求める論文なのかなと思ったんですが、違いました。下記の論文が自分が思ってたものに近いのかな？今後、読むべき課題とします。

Complete offline tuning of the unscented Kalman filter

後、論文をブログにまとめるのは「そこそこ文章が必要で大変(Google翻訳で楽しようと思ったら修正が結局大変)」かつ「制約が無いので長くなりがち」なので、発表形式のスライドにまとめた方が良いという気付きを得ました。

【論文】「LO-Net: Deep Real-time Lidar Odometry」を読む【CVPR2019】

SLAM 論文 機械学習

目次

はじめに

こんにちは．ササキ(@saitosasaki)です．
twitterに論文のまとめを書いたんですけど,ブログにも上げときます。ブログではtwitterと違って、文字数や画像制限がないので少し詳しく、かつ若干文を修正しました。

興味をもったきっかけ

lidarでdeepな位置合わせはPointNetLK(2019)があったり、deepな逐次SLAMもCNN for IMU Assisted Odometry Estimation using Velodyne LiDAR(2017)がありました。しかし、逐次SLAMで現状の逐次SLAMと同精度を謳っているのがない印象だったのでLO-Netの論文を読みました。

arxiv.org

論文

先行研究

深層学習によるライダーオドメトリはCNN for IMU Assisted Odometry Estimation using Velodyne LiDARがあったが、並進方向の推定のみ。

手法

LO(Lidar Odomery）とタイトルにはありますが、論文全体ではライダーオドメトリ(LO-Net部)とマッピングを組み合わせてた手法を提案しています。

1 ライダーオドメトリ部

ライダーオドメトリの全体図
f:id:ssk0109:20190421153745p:plain
ライダーオドメトリのネットワークアーキテクチャ f:id:ssk0109:20190421155028p:plain
ネットワークのパラメータ
f:id:ssk0109:20190421155503p:plain

  • 1.1.まずscanとscanからNormal Estimationした法線をエンコーダーに入れ、特徴量抽出。
    エンコーダー・デコーダーは図9のように障害物のマスクを予測させるように学習して、エンコーダーを特徴量抽出機として使う。 f:id:ssk0109:20190421154035p:plain

  • 1.2次に時刻t-1とtでの連続したscanの特徴量を回帰モデルに入れて、odometryを出力。

2. マッピング部

現在のodometryとscan、過去の地図と姿勢を入力に、現在の地図と姿勢を算出（ここは非ディープな処理）。
f:id:ssk0109:20190421154518p:plain

工夫

  • 1.対象点近傍の重み付き外積を用いて、法線推定を単純化。
    f:id:ssk0109:20190421154712p:plain
  • 2.軽量化のために畳み込みのほとんどをSqueezeNetで提案されたfireConvに置き換え。
    f:id:ssk0109:20190421155139p:plain

実験結果

実験はKITTIデータセットのVelodyne HDL-64を使用。
現状SOTAである非deepなLOAMを超える精度が出ている。 f:id:ssk0109:20190421154223p:plain f:id:ssk0109:20190421154356p:plain

今後の展望

  • 1.CNNに入れるために点群を前処理しているので、点群をそのまま入れるように変更。
  • 2.ground truthを教師として学習させているので、教師なしへ変更。

感想

ground truthを教師にしてるのとオドメトリを特徴量マッチングじゃなくて回帰させるのはパワープレイだなと思いました。

ベイズの定理からカルマンフィルタを導出する

Robot ベイズ

目次

はじめに

こんにちは．ササキ(@saitosasaki)です．
私はカルマンフィルタを雰囲気で使っていたため，前々からベイズの定理からカルマンフィルタがどうやって導出されるのかもよくわかっていませんでした．(最小分散推定からの導出は知ってたんですが）
しかし，ふと『確率ロボティクス』を読み返してみると普通に書いてありました．最初に読むとき飛ばして良いと書いてあったので，飛ばして読んでいたみたいです．読んでみると非常に明快で、自分の中の理解が大いに深まりました。
今回は自分の記憶に刻むために状態空間モデルが時不変かつ一次元という簡単な条件でベイズの定理からカルマンフィルタを導出してみます。

追記：制御/ロボティクス系の書籍では、片山先生の『非線形カルマンフィルタ』でもベイズの定理からカルマンフィルタの導出をしています。

そもそもベイズとは

ベイズ(確率)というものを理解するには以下のスライドがわかりやすいと思います．
5分でわかるベイズ確率

ベイズの定理に関しては以下のスライドがわかりやすいと思います．
15分でわかる(範囲の)ベイズ統計学

そもそもカルマンフィルタとは

以下の記事がグラフィカルでわかりやすいと思います．
シンプルなモデルとイラストでカルマンフィルタを直観的に理解してみる - Qiita

導出に出てくる用語について

用語は基本、以下の確率ロボティクスの展望という論文に準拠しています。 以下の論文の「2.おさらい」のマルコフ過程とベイズの公式をチェックしてください。
確率ロボティクスの展望

カルマンフィルタの導出

モデル

  • 状態遷移モデル
    x_t = a x_{t-1} + b u_t + \epsilon_t
    ここでx_tとx_{t-1}は時刻tにおける状態量で，u_tは同時刻における制御量です。また，\epsilon_tは平均0，分散rの正規分布に従うノイズです。
  • 計測モデル
    z_t=c x_t + \delta_t
    ここでz_tは時刻tにおける観測量です。また，\delta_tは平均0，分散qの正規分布に従うノイズです。

予測更新

(x_{t-1}のせいで式変形が面倒になっているため、最初は計測更新の方から読んだ方が良いかもしれないです。もしくは予測更新の部分はベイズの定理使ってないですし、飛ばしても大丈夫です。)
予測更新は1次のマルコフ性を仮定することで、以下で表せられます。

\overline{bel}(x_t) = p(x_t \vert z_{1:t-1},u_{1:t})
=\int p(x_t \vert x_{t-1},z_{1:t-1},u_{1:t}) bel(x_{t-1})dx_{t- 1}
=\int p(x_t \vert x_{t-1},u_t) bel(x_{t-1})dx_{t-\ 1}\tag{1}

ここで
状態遷移確率： p(x_t \vert x_{t-1},u_t) \sim N(x_t,a x_{t-1} + b u_t,r) \tag{2}
(平均a x_{t-1} + b u_t,分散rの正規分布)
1つ前のデータの事後信念： bel(x_{t-1}) \sim N(x_{t-1},\mu_{t-1},\sigma_{t-1}^{2}) \tag{3}
(平均\mu_{t-1},分散\sigma_{t-1}^{2}の正規分布)
です．

信念 \overline{bel}(x_t)が正規分布であることを確認する

　まず，式(1)を式(2),(3)を用いて正規分布で表わすと

\overline{bel}(x_t)=　\eta \int exp(-\frac{1}{2} r^{-1}(x_t -ax_{t-1}-bu_t)^{2}) \cdot exp(-\frac{1}{2} \sigma_{t-1}^{-2}(x_{t-1} -\mu_{t-1})^{2})dx_{t-1} \tag{4}

となります．ここで、exponentialの係数は、まとめて正規化定数ηを用いて表しています．
略記して

\overline{bel}(x_t)=\eta \int exp(-L_t)dx_{t-1} \tag{5}

とします。ここで L_t は以下で表せます．

L_t = \frac{1}{2}r^{-1}(x_t - a x_{t-1} -b u_t)^{2}+ \frac{1}{2}\sigma_{t-1}^{-2}(x_{t-1}-\mu_{t-1})^{2} \tag{6}

　式(5)はx_{t-1}についての積分を含んでおり、これを解くためには L_tを式変形します。具体的には

L_t=L_t(x_{t-1},x_t)+L_t(x_t) \tag{7}

のように分解します。こうすることでx_{t-1}に無関係な変数を、x_{t-1}についての積分から切り離すことができます。
このことに注意して\overline{bel}(x_t)を式変形すると、

\overline{bel}(x_t)=\eta \int exp(-L_t)dx_{t-1}
= \eta \int exp(-L_t(x_{t-1},x_t)-L_t(x_t))dx_{t-1}
= \eta \cdot exp(-L_t(x_t))\int exp(-L_t(x_{t-1},x_t))dx_{t-1} \tag{8}

となります。ここで\int exp(-L_t(x_{t-1},x_t))dx_{t-1}がx_tに依存しないように関数L_t(x_{t-1},x_t)を選べば、正規化定数\etaに\int exp(-L_t(x_{t-1},x_t))dx_{t-1}を組み込むことができます。そこでx_tに依存しないように関数L_t(x_{t-1},x_t)を決定していきます。
　まず、L_tの一次、二次の導関数を計算すると、

\frac{\partial L_t}{\partial x_{t-1}}=-ar^{-1}(x_t-ax_{t-1}-bu_t)+\sigma_{t-1}^{-2}(x_{t-1} -\mu_{t-1}) \tag{9}
\frac{\partial^{2} L_t}{\partial x_{t-1}^{2}}=a^{2}r^{-1}+\sigma_{t-1}^{-2}:=\Psi_t^{-1} \tag{10}

となります。\frac{\partial L_t}{\partial x_{t-1}}=0の時、 \overline{bel}(x_t)の平均値が得られるので、この等式をx_{t-1}に対して解くと、

ar^{-1}(x_t-ax_{t-1}-bu_t)=\sigma_{t-1}^{-2}(x_{t-1} -\mu_{t-1})
\Longleftrightarrow x_{t-1}=\Psi_t[ar(x_t-bu_t)+\sigma_{t-1}^{2}\mu \tag{11}

となります。この結果を利用してL_t(x_{t-1},x_t)を以下のように決めます。

L_t(x_{t-1},x_t)=\frac{1}{2}\Psi_t(x_{t-1}-\Psi_t(ar(x_t-bu_t)+\sigma_{t-1}^{2}\mu))^2 \tag{12}

このように定義すれば、

det(2\pi\Psi)^{-\frac{1}{2}}exp(-L_t(x_{t-1},x_t)) \tag{13}

は変数x_{t-1}に対する確率密度関数になります。つまりこれは

\int det(2\pi\Psi)^{-\frac{1}{2}}exp(-L_t(x_{t-1},x_t))dx_{t-1}=1 \tag{14}

が成り立つということです。よってL_t(x_{t-1},x_t)はx_tに依存しないためL_tの正規化定数\etaに\int exp(-L_t(x_{t-1},x_t))dx_{t-1}を組み込むことができることがわかりました。よって\overline{bel}(x_t)は以下のように変形できます。

\overline{bel}(x_t) = \eta \cdot exp(-L_t(x_t))\int exp(-L_t(x_{t-1},x_t))dx_{t-1}
= \eta \cdot exp(-L_t(x_t)) \tag{15}

次にまだL_t(x_t)を決定していないので決定します。L_t(x_t)は以下で決定できます。

L_t(x_t) = L_t - L_t(x_{t-1},x_t)
=\frac{1}{2}r(x_t-ax_{t-1}-bu_t)^{2}+\frac{1}{2}r(x_{t-1}-\mu_t)^{2}-\frac{1}{2}\Psi_t(x_{t-1}-\Psi_t[ar(x_t-bu_t)+\sigma_{t-1}^{-2}\mu)^{2} \tag{16}

ここで\Psi_t=(a^{2}r^{-1}+\sigma_{t-1}^{-2})^{-1}を用いてx_{t-1}を消去すると

L_t(x_t) =\frac{1}{2}r^{-1}(x_t-bu_t)^{2} +\frac{1}{2}\mu_{t-1}^{2}\sigma_{t-1}^{-2}-\frac{1}{2}(a^{2}r^{-1}+\sigma_{t-1}^{-2})(ar^{-1}(x_t-bu_t)+\sigma_{t-1}^{-2}\mu_{t-1})^{2} \tag{17}

となります。L_t(x_t)はx_tの二次関数なので、\overline{bel}(x_t)は正規分布だとわかります。この分布の平均値と共分散は「L_t(x_t)が最小値の時のx_t」と「L_t(x_t)の曲率」にあたります。
（ここ、「なんで？」って思う方がいるんですが、正規分布の式を考えれば自然とわかると思います。）

信念 \overline{bel}(x_t)の平均値と共分散を求める

　まず、この分布の平均値を求めていきます。 L_t(x_t)の一次導関数は

\frac{\partial L_t(x_t)}{\partial x_{t}}=r^{-1}(x_t-bu_t)-r^{-1}a(a^{2}r^{-1}+\sigma_{t-1}^{-2})^{-1}(a r^{-1}(x_t-bu_t)+\sigma_{t-1}^{-2}\mu_{t-1}
=(r^{-1}-r^{-2}a^{2}(a^{2}r+\sigma_{t-1}^{-2})^{-1})(x_t-bu_t)-r^{-1}a(a^{2}r+\sigma_{t-1}^{-2})^{-1}\sigma_{t-1}^{-2}\mu_{t-1}
=(r+a^{2}\sigma_{t-1})^{-2}(x_t-bu_t)-r^{-1}a(a^{2}r^{-1}+\sigma_{t-1}^{-2})^{-1}\sigma_{t-1}^{-2}\mu_{t-1} \tag{18}

となります。 L_t(x_t)の最小値は\frac{\partial L_t(x_t)}{\partial x_{t}} \vert_{x_t=\overline{\mu_t}}=0の時に得られるので、この等式を\overline{\mu_t}について解くと

\overline{\mu_t}=bu_t+(r+a^{2}\sigma_{t-1}^{2})r^{-1}a(a^{2}r+\sigma_{t-1}^{-2})^{-1}\sigma_{t-1}^{-2}\mu_{t-1}
=bu_t+a(1+\sigma_{t-1}^{2}a^{2}r)(\sigma_{t-1}^{2}a^{2}r+1)^{-1}\mu_{t-1}
=bu_t+a\mu_{t-1} \tag{19}

となります。
　次に、\overline{bel}(x_t)の共分散を求めます。\frac{\partial^{2} L_t(x_t)}{\partial x_{t}^{2}}の逆数が共分散になるので、二次導関数は式(18)を微分して

\frac{\partial^{2} L_t(x_t)}{\partial x_{t}^2}=(a^{2}\sigma_{t-1}^{2}+r)^{-1} \tag{20}

となります。以上より予測更新の式は

\overline{\mu_t}=a\mu_{t-1}+bu_t \tag{19}
\overline{\sigma_t^{2}}=a^{2}\sigma_{t-1}^{2}+r \tag{20}

となります。

計測更新

計測は過去には依存しないという仮定の基、計測更新はベイズの定理から正規化定数\etaを用いて以下で表せられます。

bel(x_t)=\eta p(z_t \vert x_t,z_{1:t-1},u_{1:t}) \overline{bel}(x_t)
=\eta p(z_t \vert x_t) \overline{bel}(x_t) \tag{21}

ここで
計測確率： p(z_t \vert x_t) \sim N(z_t,c x_t,q) \tag{22}
(平均c x_{t} ,分散qの正規分布)
予測更新で求めた事前信念： \overline{bel}(x_t) \sim N(x_{t},\overline{\mu_{t}},\overline{\sigma_{t}^{2}}) \tag{23}
(平均\overline{\mu_{t}},分散\overline{\sigma_{t}^{2}}の正規分布)
です。
bel(x_t)を正規分布で表わすと

bel(x_t)=\eta p(z_t \vert x_t) \overline{bel}(x_t)
= ηexp(-J_t) \tag{24}

ここで、J_tは以下の通りです。

J_t=\frac{1}{2}q^{-1}(z_t-cx_t)^{2}+\frac{1}{2}\overline{\sigma_t^{2}}^{-1}(x_t-\overline{\mu_t})^{2} \tag{25}

J_tはx_tの二次関数なので、bel(x_t)は正規分布だとわかります。なので今回もJ_tの一次導関数を求めてbel(x_t)の平均値\mu_tを求めます。

\frac{\partial J_t}{\partial x_{t}}=-cq^{-1}(z-cx_t)+\overline{\sigma_t^{2}}^{-1}(x_t-\overline{\mu_t}) \tag{26}

\frac{\partial J_t}{\partial x_{t}} \vert_{x_t=\mu_t}=0を解くと、

cq^{-1}(z_t-c\mu_t)=\overline{\sigma_t^{2}}^{-1}(\mu_t-\overline{\mu_t})
\Longleftrightarrow \mu_t=\overline{\mu_t}+\sigma_t^{2}cq^{-1}(z_t-c\overline{\mu_t}) \tag{27}

ここでカルマンゲイン

K_t=\sigma_t^{2}cq^{-1} \tag{28}

を定義すると\mu_tは以下のようになります。

\mu_t=\overline{\mu_t}+K_t(z_t-c\overline{\mu_t}) \tag{29}

　次に、bel(x_t)の共分散を求めます。\frac{\partial^{2} J_t(x_t)}{\partial x_{t}^2}の逆数がbel(x_t)の共分散になるので、二次導関数は

\frac{\partial^{2} J_t(x_t)}{\partial x_{t}^{2}}=c^{2}q^{-1}+\overline{\sigma_t}^{-2} \tag{30}

となります。以上よりbel(x_t)の共分散\sigma_t^{2}は

\sigma_t^{2}＝（c^{2}q^{-1}+\overline{\sigma^{2}}_t^{-1})^{-1} \tag{31}

先ほど求めたカルマンゲインですが、事後信念の共分散\sigma_tを用いるのは計算上不便なので、上式より事前信念の共分散\overline{\sigma_t}を用いた式に書き換えます。

K_t=\sigma_t^{2}cq^{-1}
=（c^{2}q^{-1}+\overline{\sigma}_t^{-2})^{-1}cq^{-1}
=\overline{\sigma^{2}}_tc(c^{2}\overline{\sigma^{2}}+q)^{-1} \tag{32}

またカルマンゲインを用いて、\sigma_t^{2}を書き換えると、

\sigma_t^{2}＝（c^{2}q^{-1}+\overline{\sigma_t^{2}}_t^{-1})^{-1}
=(1-\overline{\sigma_t}c^{2}(q+c^{2}\overline{\sigma_t^{2}})^{-1})\overline{\sigma_t^{2}}
=(1-K_tc)\overline{\sigma_t}^{2} \tag{33}

となります。
以上より、観測更新の式は

K_t=\overline{\sigma_t^{2}}_tc(c^{2}\overline{\sigma_t^{2}}+q)^{-1} \tag{32}
\mu_t=\overline{\mu_t}+K_t(z_t-c\overline{\mu_t}) \tag{29}
\sigma_t^{2}=(1-K_tc)\overline{\sigma_t^{2}} \tag{33}

となります．

カルマンフィルタの式まとめ

まとめると以下のようになります。

予測更新

平均値：\overline{\mu_t}=a\mu_{t-1}+bu_t
分散： \overline{\sigma_t^{2}} = a^{2} \sigma_{t-1} ^{2}+ r

計測更新

カルマンゲイン：K_t=\overline{\sigma}^{2}_tc(c^{2}\overline{\sigma_t}^{2}+q)^{-1}
平均値：\mu_t=\overline{\mu_t}+K_t(z_t-c\overline{\mu_t})
分散：\sigma_t^{2}=(1-K_tc)\overline{\sigma_t^{2}}

参考文献

  • 訳：上田、著：S.スラン et all,"確率ロボティクス 3.2.4 カルマンフィルタの数学的導出"

関連記事

ssk0109.hatenablog.com

『確率ロボティクス』の練習問題を解いてベイズの定理を理解する

Robot ベイズ

目次

はじめに

ことの発端は自分のtwitterのタイムラインに流れてきた以下のtweetです．

これをきっかけに「自分もカルマンフィルタを使って色々してきたけど，よく考えるとあまり理解していない！カルマンフィルタを勉強し直そう！」と思いました．
カルマンフィルタはベイズフィルタの一種です．多分自身のベイズの理解が甘いと思うので，まずは確率ロボティクスの練習問題がrecursiveなベイズを理解する上で良問なので改めて解いてみました。
余談ですが初めてtex使ったんですけど、分からな過ぎて辛かったです

ベイズの定理

以下、ベイズについての軽い説明をします．

ベイズ確率とは

ベイズ確率の直感的理解には以下のスライドが詳しいです．
コインと男女の例など導入からわかりやすいです。
頻度主義と違ってベイズ主義は主観の信念の度合いを確率にしているものなのだとわかります。
5分でわかるベイズ確率

ベイズの定理

ある事象Xが起こるという条件で別の事象Yがおこる確率 P(Y|X)はベイズの定理より以下になります．
P(Y|X)= \frac{P(X|Y) P(Y)}{P(X)}
ここで， P(Y)は事前確率， P(Y|X)は事後確率， P(X|Y)を尤度， P(X)は正規化定数（周辺尤度・エビデンスとも呼ばれる）と呼びます．
正規化定数は P(X)=P(X|Y) P(Y) + P(X|\overline{Y}) P(\overline{Y})で表されます．
ベイズ更新は尤度を通して事前確率を事後確率に更新することです．

データの追加

上のベイズの定理にZが追加で与えられた場合，以下のようになります．
P(Y|X,Z)= \frac{P(Z|X,Y) P(Y|X)}{P(Z|X)}
事前確率がZ追加前の事後確率になっているのがポイントです．

問題(2章8節の問1)

問題内容

以下の場合に，n回の計測が全て1[m]以下であるデータ列z_{1:n}(=(z_1 z_2 ... z_n))に対し，センサが壊れている確率 P(A|z_{1:n})を求め，n=1~10の時の値を計算する。

  1. あるロボットが0[m]から3[m]の範囲まで計測できる距離センサを装備している。
  2. 計測対象がロボットの前方0〜3[m]の間で一様ランダムに出現する。
  3. 壊れたセンサは常に実際の距離に関係なく1[m]未満の値を出力し続ける。
  4. センサが壊れている確率P(A)は0.01(=p)だと知っている．

答案

ベイズの式より
P(A|z_{1:n})= \frac{P(z_n|A,z_{1:n-1}) P(A|z_{1:n-1})}{P(z_n|z_{1:n-1})}
= \frac{P(z_n|A,z_{1:n-1}) (1 \cdot P(A))}{P(z_n|z_{1:n-1})} （問題文3より，再帰的に求まる）
= \frac{1 \cdot p}{P(z_n|z_{1:n-1})} (問題文4より)
= \frac{p}{P(z_n|A,z_{1:n-1}) P(A|z_{1:n-1}) + P(z_n|\overline{A},z_{1:n-1}) P(\overline{A}|z_{1:n-1})}(正規化定数の変形)
= \frac{p}{P(z_n|A,z_{1:n-1}) (1 \cdot P(A)) + P(z_n|\overline{A},z_{1:n-1}) (\frac{1}{3^{n-1}} \cdot P(\overline{A}))}（問題文2~3より，再帰的に求まる）
= \frac{p}{1 \cdot p+ \cdot \frac{1}{3} \frac{1}{3^{n-1}} (1-p)} (問題文2~4より)
= \frac{p}{p+ \frac{1}{3^{n}} (1-p)}

解

P(A|z_{1:n})= \frac{p}{p+ \frac{1}{3^{n}} (1-p)}
p=0.01より

n 確率
1 1/34 =0.0294...
2 1/12 =0.0833...
3 3/14 =0.2143...
4 9/20 =0.4500...
5 27/38 =0.7105...
6 81/92 =0.8804...
7 243/254 =0.9567...
8 729/740 =0.9851...
9 2188/2198 =0.9950...
10 6561/6572=0.9983...

参考にした資料

関連記事

ssk0109.hatenablog.com

【論文】「Visual SLAM: Why Bundle Adjust?」を読む【ICRA2019】

論文 SLAM

はじめに

興味をもったきっかけは以下のtweetです。

vSLAMはSLAMの中でも更に全然わからないのですが、バンドル調整(Bandle Adjustment)(某界隈でBAと略すらしい）を使ってないのは興味深いです。なので、論文を読むことにしました。
気合で一通り目を通しましたが、軽い気持ちで読むんじゃなかったと後悔しました。

[1902.03747] Visual SLAM: Why Bundle Adjust?

概要

バンドル調整に基づくＳＬＡＭの問題点

  • バンドル調整を慎重に初期化する必要があり、複雑。
  • (十分なベースラインが必要なので、）スローモーションまたは純粋な回転モーションが苦手 。

提案手法

バンドル調整の代わりに、カメラの向きだけを徐々に最適化するために回転の平均化(rotation averaging)を行う。
提案手法により、位置と三次元地図をキーフレームレートで推定および維持する必要がなくなるだけでなく（よりシンプルなSLAMシステムになるだけでなく）、 スローモーションや純粋な回転モーションにも対応できるようになる。

本文

序論

従来のBA(Bandle Adjustment) SLAM

f:id:ssk0109:20190213102201p:plain:w300

ここで、
ui, j is the 2D coordinates of the i-th scene point as seen in the j-th image Zj.
structure-from-motion (SfM) aims to estimate the 3D coordinates X = {Xi} of the scene points and 6DOF poses {(Rj,tj)} of the images {Zj}.

bundle adjustment (BA) formulation

f:id:ssk0109:20190213105305p:plain:w300

提案手法 L-INFINITY SLAM

f:id:ssk0109:20190213101952p:plain:w300　　

rotation averaging formulation

Given a set of relative rotations {Rj,k} between pairs of overlapping images {Zj ,Zk}, the goal of rotation averaging is to estimate the absolute rotations {Rj}

f:id:ssk0109:20190213102554p:plain:w300

f:id:ssk0109:20190213102729p:plain:w300
Unlike (1) which minimises the sum of squared reprojection error,
(4) minimises the maximum reprojection error.

アルゴリズム詳細

A. Estimating relative motions

Rj,k はrotationally aligning backprojected feature rays by using a rotation only variant of Trimmed ICPで推定している。

B. Rotation averaging

式(3)を解くために an iteratively reweighted least-squares approach in SO(3)を使用。

C. Known rotation problem

By referring to R(1:2)j as the first two rows of Rj, and to R(3)j
as the third row of Rj (similarly for t(1:2) and t(3)), the projection of Xi onto the j-th image is given by

f:id:ssk0109:20190214011930p:plain:w300
式(6)を式(4)に適用し式変形すると、以下の最適化問題になる。 f:id:ssk0109:20190214012152p:plain:w300
f:id:ssk0109:20190214012716p:plain:w300

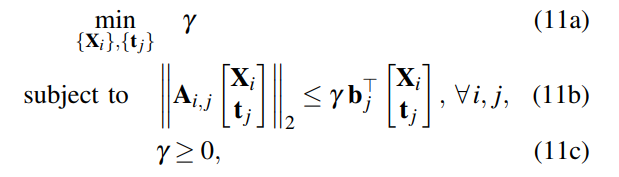
これをRes-Intと呼ばれる方法で解く。Res-Intはこの問題を about 3 seconds for moderate size input (around 15 images and 3000 3D points)で解く。
Res-Int はLine 5 in Algorithm 2の the known rotation prob routine に当たる。

D. Known rotation(KRot) problem with translation direction constraints

ループが検出される時入力サイズは大きくなるので、Step 9 in Algorithm 2のKRotを解くには非常に時間がかかる。
そこで、カメラの並進方向を組み込んだ定式化を使用して、入力のサンプルに対するループクロージャを解決することを提案する。
カメラ位置の制約は以下で表わせられる。
f:id:ssk0109:20190214020429p:plain:w300
式(12)はKnown rotation problem において式(13)の角度制約に一致する。

f:id:ssk0109:20190214020906p:plain:w300

Known rotation problemに角度制約を追加すると以下が導出される。
これによりスパースな３Ｄ点集合を用いてループクロージャ（＜１００秒）を効率的に解くことが可能になる。

f:id:ssk0109:20190214021941p:plain:w300

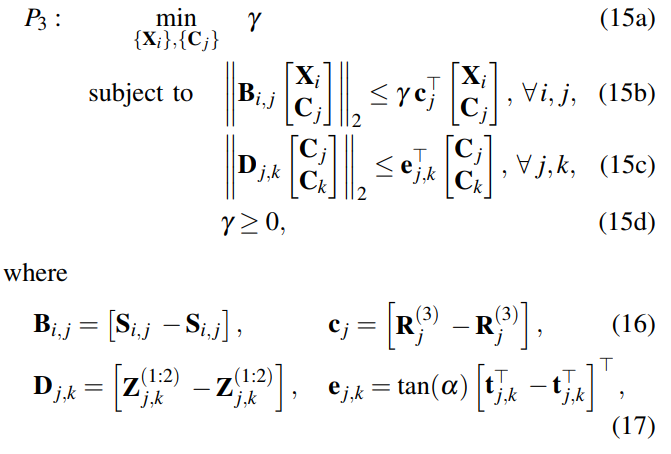
ここでZj,kは以下のような回転行列である。

f:id:ssk0109:20190214021342p:plain:w300

結果

  • 誤差低減
    従来のBandle Adjustmentだとトラッキングに失敗している箇所がある。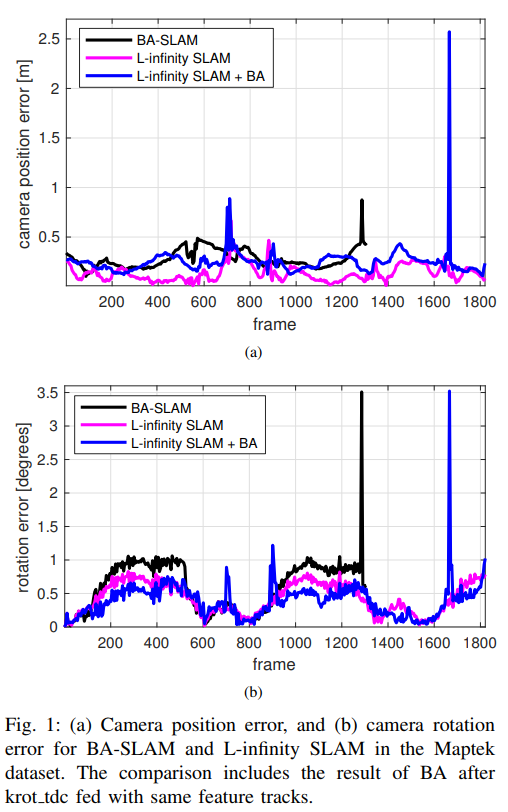 f:id:ssk0109:20190213103938p:plain:w300

  • 軌跡が滑らかに
    f:id:ssk0109:20190213103711p:plain:w300

  • 実行時間の高速化
    f:id:ssk0109:20190213104055p:plain:w300

読むときに参考にした資料

vSLAMの勉強用

論文理解用

今後の読むべき論文

  • rotation averagingの論文
  • Res-Intの論文

追記

解説スライドを挙げてくれた方がいたので、追記しときます。
Visual SLAM: Why Bundle Adjust?の解説（第4回3D勉強会@関東）

Google Cartographerとgmappingの比較

Robot SLAM ROS Cartographer

はじめに

こんにちは．ササキ(@saitosasaki)です． レーザSLAMのSOTA(State Of The Art)(所説ある)のOSS(Open Source Software)であるCartographerですが、実際使ってみると性能が出ないという話を聞いたり、良さがわかりづらい印象を受けます。

github.com

そこで、Cartographerは有名なgmappingに比べ何が良いのか調べてまとめました！

違い

違いはループ閉じ込み(loop closure)が明示的か非明示的かにあります。
ループ閉じ込みは、再訪点（前に訪れたことがある地点）検出を陽に行う方法と行わない方法があります。
gmappingは再訪点検出を陽に行いません。
Cartographerは再訪点検出を陽に行います。

gmapping

gmappingはrosのnavigationパッケージにもある有名なベイズフィルタ系のSLAMです。

github.com

gmappingはRBPF(Rao-Blackwellized ParticleFilter)-SLAMの代表例です。
PF(Particle Filter)には次元の呪いの問題があり、ロボット位置と地図をPFで推定すると、次元の指数乗で計算量が増加してしまいます。
そこでRBPF-SLAMはロボット位置と地図を分離して、位置推定のみにParticle Filterを使用し、地図推定は他の手法で解析的に求めます。1個の仮設(パーティクル）に1個の地図を割り当てているイメージです。
RBPF-SLAMでは、再訪点検出を明示的に行わず、多数の仮設の中で再訪点の近くを通る仮説の評価値（尤度関数の値）が高くなり、パーティクルフィルタによって評価値の高いものが選択されることでループ閉じ込みを行います。しかし、屋外等の大規模な環境といった条件によっては、多くの仮説を生成しないと仮説が再訪点をうまく通らないことがあり，ループが閉じません。

Cartographer

Cartographerはグリッドベースのスキャンマッチングによる逐次SLAMと一括処理のグラフベースSLAMの二種類で構成されています。
グラフベースSLAMでは、明示的に再訪点を検出します．具体的に言うと，現在地点の形状が過去の地図のある地点の形状と一致しているかを探索し，その地点が再訪点か判断します。
再訪点を発見した場合，再訪点と現在地が一致するという拘束をかけ、ロボット軌跡の最適化を行います。

Cartographerによるループ閉じ込みの動画
www.youtube.com

Cartographerの何が良くないのか

しかし、Cartographerは逐次SLAMは普通のスキャンマッチングです．（むしろ凡．特に小規模な環境においては ，パーティクルフィルタでロバストな位置推定ができるgmappingと比べるのは酷な話です．)
また，大規模環境でのポーズ調整も大変で、パラメータ調節しないとsotaの癖になかなか精度が出ません。
"Cartographer と Autowareを用いた自律走行" によると、屋外のパラメータ調整では

  • （性能の良い）オドメトリの寄与（を上げる）
    対応するパラメータはpose_graph.luaの以下。
odometry_translation_weight   
odometry_rotation_weight
  • ループ検出（範囲）の拡大
    対応するパラメータは上と同様にpose_graph.luaの以下です。
max_constraint_distance（defautだと15mx15m)

が必要であるとあります。

まとめ

Cartographerは明示的なループ閉じ込みがあるのは良いが、逐次SLAMがあまり良くない。
屋外等でも使いたかったら、良いオドメトリを買ってオドメトリの寄与を上げ、ループ検出の拡大範囲を上げる等のパラメータチューニングをする必要がある。

追記(重要)

上の記事は2019年3月以前の情報を基に書いているのですが、 原先生が2019年12月15日の第６回　3D勉強会＠関東で発表されたスライドによると、つくチャレ2019で更にCartographerを使い込んだ経験から、オドメトリよりもループの拘束が適切に生成できているかが重要だそうです。また、各種パラメータチューニングに関しても細かく書いてあります。

www.slideshare.net

参考資料

本文を書く際に参考にしたもの

原 祥尭,"確率的に蓄積したスキャン形状により過去を考慮した Rao-Blackwellized Particle Filter SLAM",2015
友納正裕,移動ロボットの環境認識 —地図構築と自己位置推定",2016
友納正裕,"SLAM入門",2018
原 祥尭,"オープンソースSLAMの分類",2018
原 祥尭,"Cartographer と Autoware を用いた自律走行",2018

論文&ソースを理解する際に参考にしたもの

Real-Time Loop Closure in 2D LIDAR SLAM,2016
github.com/googlecartographer/cartographer
自律移動ロボットのためのグリッドマップ作成MATLAB, Pythonサンプルプログラム - MyEnigma
Googleが開発しているC++最適化ライブラリCeres Solverの使い方とサンプルコード - MyEnigma

関連記事

ssk0109.hatenablog.com

ssk0109.hatenablog.com

ssk0109.hatenablog.com