ROS dashingが今までのROS2と比べてLTS(Long Time Support)期間が長くなって、自分の中でROS2を勉強する機運が高まってきました。
ROS Japan UG(User Group)が開催しているROS勉強会のROS2チュートリアルがcrysterl対応でdashingに対応してなかったので、勉強がてらdashingで動かしました。

ROS2勉強会@東京
rosjp.connpass.com

ROS2勉強会@大阪
rosjp.connpass.com

ROS2チュートリアル資料。これをやりました。
gbiggs.github.io

コード置き場

修正したコード。style_comparisonブランチにあります。

github.com

環境

ubuntu 18.04

トラブルシューティング

別に見る必要は無いです。一応書き残しときます。

問題1：rclcpp_register_node_pluginsコマンド

エラーメッセージ

CMake Error at CMakeLists.txt:32 (rclcpp_register_node_plugins):
  Unknown CMake command "rclcpp_register_node_plugins".

対処法
dashingではrclcpp_register_node_pluginsコマンドの代わりにrclcpp_components_register_nodesコマンドになったので、CMakeListsを修正。 github.com

問題2：create_subscription関数

警告メッセージ

/home/sasaki/ros2_basics/src/displayer/src/displayer_component.cpp:17:66: warning・・・  
/opt/ros/dashing/include/rclcpp/node_impl.hpp:139:1: note: declared here
 Node::create_subscription(
 ^~~~

対処法
ソース内のcreate_subscriptionの引数の修正。
以下、サイトより仕様変更の該当箇所。
ROS 2 Dashing Diademata (codename ‘dashing’; May 31st, 2019)

f:id:ssk0109:20190721210959p:plain

問題3：メッセージをpublishする際の警告

警告メッセージ

/home/sasaki/ros2_basics/src/rosjp_ros2_basics/greeter_ros2_style/src/greeter_component.cpp: In member function ‘void greeter_ros2_style::Greeter::broadcast_greeting()’:
/home/sasaki/ros2_basics/src/rosjp_ros2_basics/greeter_ros2_style/src/greeter_component.cpp:44:25: warning:・・・  
・・・  
/opt/ros/dashing/include/rclcpp/publisher.hpp:137:3: note: declared here
   publish(const std::shared_ptr<const MessageT> & msg)
   ^~~~~~~

対処法
/opt/ros/dashing/include/rclcpp/publisher.hppの137行を見に行ったら、 " If using a shared_ptr, use publish(*msg)." って書いてあったので、ソースのpublishしている部分を以下のように修正しました。

-publisher->publish(greeting)  
+publisher->publish(*greeting)

結果

左画面がpublisherのgreeterで、右画面がsubscriberのdisplayerです。
f:id:ssk0109:20190721204855p:plain

2019-06-22

Ensemble Kalman Filter(EnKF)による自己位置推定のプログラム

Robot 制御工学

宣伝

技術記事投稿サイトのQiitaに記事書きました．
Ensemble Kalman Filter(EnKF)によるランドマークベースで自己位置推定するプログラムを書いたので、その説明です．
EnKFはKalman Filterの派生アルゴリズムです．

Qiita記事 qiita.com

結果
f:id:ssk0109:20190716054334g:plain

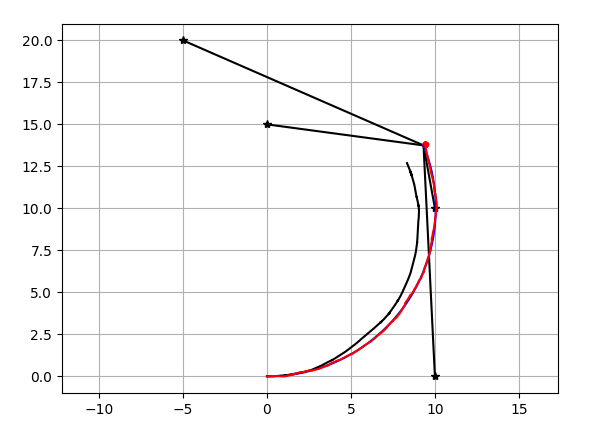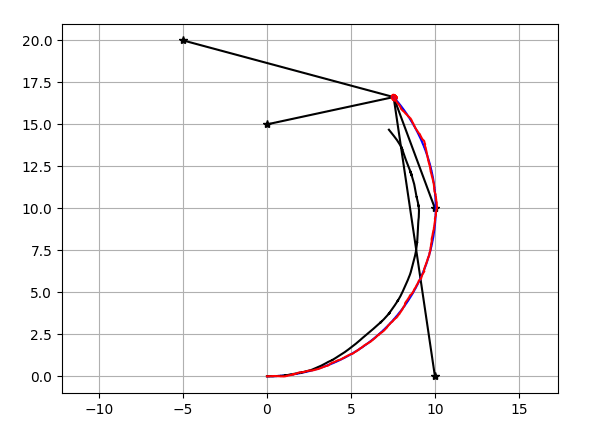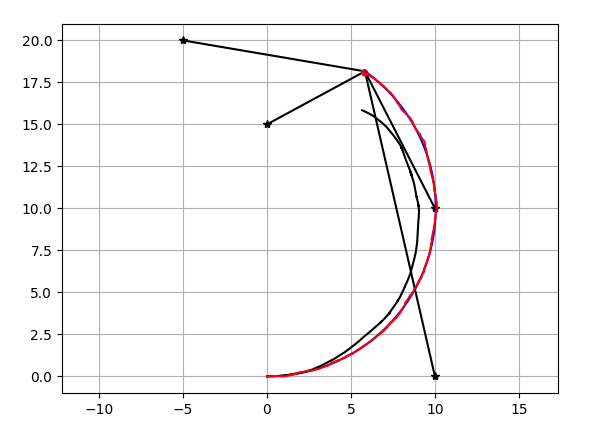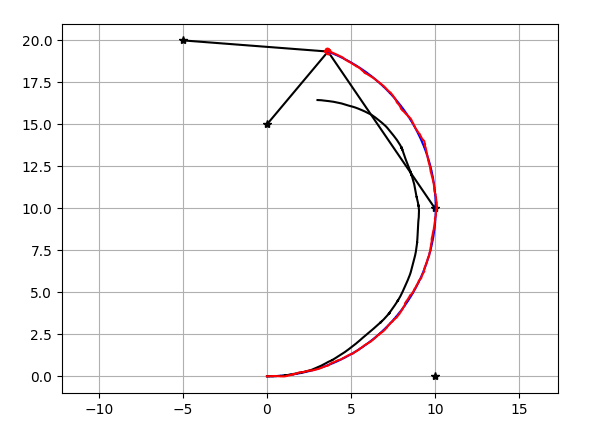
コード置き場

github.com

追記

PythonRoboticsを作った方に誘われて，PythonRoboticsにコミットしました．嬉しい．

PythonRobotics/ensemble_kalman_filter.py at master · AtsushiSakai/PythonRobotics · GitHub

2019-06-06

State Lattice Plannerのアルゴリズム解読 [PythonRobotics]

Robot 制御工学

はじめに

PythonRoboticsのstate_lattice_plannerのソースと関連論文を読んだ~~かつState Lattice Plannerを説明してる日本語記事があまりなかった~~ので，ソースを基にアルゴリズムの説明をします．

PythonRoboticsにおけるState Lattice Plannerのソースコード
 PythonRobotics/PathPlanning/StateLatticePlanner at master · AtsushiSakai/PythonRobotics · GitHub
論文
State Lattice Planner
State space sampling of feasible motions for high-performance mobile robot navigation in complex environments
Model Predictive Trajectory Generation(State Lattice Planner内で軌道生成のために用いられている手法)
Optimal Rough Terrain Trajectory Generation for Wheeled Mobile Robots

ちなみにState Lattice Plannerは千葉工業大学のfuroでも使われていて，その機体は公道で行われる自律ロボットの走行公開実験であるつくばチャレンジを完走しています． (私が興味を持ったきっかけ）
Cartographer と Autoware を用いた自律走行

f:id:ssk0109:20190627170858p:plain

State Lattice Plannerとは

State Lattice Plannerの概要に関しては以下を参照ください．
State Lattice Plannerの概要とPythonサンプルコード - MyEnigma

　State Lattice Plannerの説明を上の記事から引用します．

経路生成のフローとしては、まずはじめに複数の最終状態をサンプリングし、それぞれの状態に対してModel Predictive Trajectory Plannerでパスを引きます。そしてそれぞれのパスに対して、衝突チェックを実施し、衝突しないパスの中で、最もコストが低いパスを最終コースとして選択します。

今回は状態を位置姿勢 $\textbf{x}=(x,y,yaw)^T$ としています．
最終状態のサンプリング手法に関しては大きく3つあるのですが，本記事では簡単なUniform Polar samplingでアルゴリズムの説明をします．
また，Model Predictive Trajectory Generationに関しては，以下の記事を参照ください．
Model Predictive Trajectory Generationの概要とPythonサンプルコード - MyEnigma
上で言及されているModel Predictive Trajectory Generationは車両の運動モデルを基にパラメータを最適化し，パラメータからパスを生成する手法です．今回，最適化しているパラメータ $\textbf{p}$ はパスの長さ $s$ ，中間ステアリング角 $k_m$ ，終端ステアリング角 $k_f$ の3個です．

アルゴリズムの流れ

状態量： $\textbf{x}=(x,y,yaw)^T$
最適化するパラメータ： $\textbf{p}=(s,k_m,k_f)^T$

1. 終端状態のサンプリングステップ(Sampling)

Uniform Polar samplingの場合，画像1のように扇状に等間隔で $5(=n_{xy})$ 個の点をサンプリングします．各点毎に異なる $3(=n_h)$ 個の向きの終端状態があります．この終端状態をどうサンプルするかでUniform Polar sampling，Biased Polar sampling，Lane samplingを使い分けます．

画像1. 初期状態（左端)と終端状態

サンプルされる終端状態は以下の設定パラメータで決定されます．
設定パラメータ
$n_{xy} = 5$ (終端状態を扇状に何個とるか）
$n_h = 3$ (ある1つの終端状態の位置に関して車両の向きを何個求めるか）
$d = 20$ ( $y=0$ にある終端状態と初期状態間の長さ)
$-45^\circ \leqq a \leqq 45^\circ$ (終端状態をサンプルするための扇の角度の範囲)
$-45^\circ \leqq p \leqq 45^\circ$ (終端状態の車両の向きの範囲）

2. パス生成ステップ(Trajectory Generation)

各終端状態ごとに，Model Predictive Trajectory Generationでパラメータ $\textbf{p}=(s，k_m，k_f)^T$ を最適化し，パスを生成していきます。

2.1 初期パラメータ決定

「あらかじめある程度の数の終端状態に対して、パラメータ $\textbf{p}$ が既に計算されたLookup Table」内におけるパスのゴールが目標とする終端状態に最も近いパスのパラメータを初期値とします．こうすることで最適化の収束を早める効果があります．

lookup table(ある $x,y,yaw$ に対して $s,k_m,k_f$ をModel Predictive Trajectory Generationであらかじめ計算したもの)の一部

x	y	yaw	s	km	kf
1.0	0.0	0.0	1.0	0.0	0.0
0.9734888894493215	-0.009758406565994977	0.5358080146312756	0.9922329557399788	-0.10222538550473198	3.0262632253145982
10.980728996433243	-0.0003093605787364978	0.522622783944529	11.000391678142623	0.00010296091030877934	0.2731556687244648
16.020309241920156	0.0001292339008200291	0.5243399938698222	16.100019813021202	0.00013263212395994706	0.18999138959173634
20.963495745193626	-0.00033031017429944326	0.5226120033275024	21.10082901143343	0.00011687467551566884	0.14550546012583987
6.032553475650599	2.008504211720188	0.5050517859971599	6.400329805864408	0.1520002249689879	-0.13105940607691127
10.977487445230075	2.0078696810700034	0.5263634407901872	11.201040572298973	0.04895863722280565	0.08356555007223682
15.994057699325753	2.025659106131227	0.5303858891065698	16.200300421483128	0.0235708657178127	0.10002225103921249
20.977228843605943	2.0281289825388513	0.5300376140865567	21.20043308669372	0.013795675421657671	0.09331700188063087
25.95453914157977	1.9926432818499131	0.5226203078411618	26.200880299840527	0.00888830054451281	0.0830622000626594
0.9999999999999999	0.0	0.0	1.0	0.0	0.0

画像2：lookup tableを基にパスを生成したもの f:id:ssk0109:20190627112821p:plain

2.2 パラメータ最適化

2.2.1 パス生成

パラメータ $\textbf{p}$ ，初期ステアリング角 $k_0$ ,時間刻み $dt$ を基にステアリング角の時系列 $k_{p}=(k_{p1},k_{p2},...,k_{pi},…,k_{pf})$ をquandratic interpolationで生成し，その後，制御モデルで位置姿勢 $\textbf{x}=(x,y,yaw)^T$ の時系列であるパス $\textbf{x(p)}=(\textbf{x}_\textbf{1} \textbf{(p)},\textbf{x}_\textbf{2} \textbf{(p)},...,\textbf{x}_\textbf{i} \textbf{(p)},…,\textbf{x}_\textbf{f} \textbf{(p)})$ を生成します．

制御モデル
$x_{i+1} = x_{i} + v \cdot cos(yaw_{i}) \cdot dt$
$y_{i+1} = y_{i} + v \cdot sin(yaw_{i}) \cdot dt$
$yaw_{i+1} = yaw_{i} + v/L \cdot tan(k_{pi}) \cdot dt$
ここで，
$L=1.0(m)$ ：ホイールベース
$v=10.0/3.6(m/s)$ ：速度(一定と仮定)
$dt= ds/v$ ：時間刻み
$ds=0.1(m)$ ：距離刻み

2.2.2 閾値チェック

生成したパスに関するコストを計算し，閾値以下なら対象の終端状態でのパス生成を終了し，残りの終端状態のパス生成に移ります．PythonRoboticsでは，コストは生成したパスのゴールの位置姿勢 $x(p)_{f}$ と目標となる終端状態の位置姿勢 $x_f$ 間のノルムとなっています．

2.2.3 パラメータ調整

コストが閾値以上なら，ニュートン法を基にパラメータを変化させ，パスを再計算します．(2.2.2に戻る)

ニュートン法
$\Delta p = -(\frac{\partial \Delta x_f(p)}{\partial p})^{-1} \Delta x_f(p)$
$p_{new} = p_{old} + \alpha \Delta p$

ここで，
$\Delta x_f(p)=(x_f - x(p)_{f})$
$\alpha$ ：学習率
また，ヤコビアン $\frac{\partial \Delta x_f(p)}{\partial p}$ は解析的に計算できないので、以下のように中心差分で数値的に求めます．

$\frac{\partial \Delta x_f(p)}{\partial p}= \begin{pmatrix} \frac{x_f(s+h_s,k_m,k_f)-x_f(s- h_s,k_m,k_f)}{2h_s} &\frac{x_f(s,k_m+h_{km},k_f)-x_f(s,k_m-h_{km},k_f)}{2h_{km}} &\frac{x_f(s,k_m,k_f+h_{kf})-x_f(s,k_m,k_f-h_{kf})}{2h_{kf}} \\\ \frac{y_f(s+h_s,k_m,k_f)-y_f(s- h_s,k_m,k_f)}{2h_s} &\frac{y_f(s,k_m+h_{km},k_f)-y_f(s,k_m-h_{km},k_f)}{2h_{km}} &\frac{y_f(s,k_m,k_f+h_{kf})-y_f(s,k_m,k_f-h_{kf})}{2h_{kf}} \\\ \frac{yaw_f(s+h_s,k_m,k_f)-yaw_f(s- h_s,k_m,k_f)}{2h_s} &\frac{yaw_f(s,k_m+h_{km},k_f)-yaw_f(s,k_m-h_{km},k_f)}{2h_{km}} &\frac{yaw_f(s,k_m,k_f+h_{kf})-yaw_f(s,k_m,k_f-h_{kf})}{2h_{kf}} \end{pmatrix}$

ここで，
$x_f(s,k_m,k_f)=x_f(p)$
$h=(h_{s},h_{km},h_{kf})^{T}=(0.5,0.02,0.02)^{T}$ ：パラメータ摂動

3. パス選択ステップ

画像3のように生成されたパス群の中から各パスに対して衝突チェックをし，なんらかの指標を基に最適なパスを選択します．PythonRobotisでは，衝突チェック・パス選択まではしていません．

画像3.パス生成結果

参考にしたもの

lattice_planner · master · Autoware Foundation / Autoware.AI / core_planning · GitLab

https://blog.csdn.net/yuxuan20062007/article/details/82330165

2019-06-01

Udacityにある自動運転ソフトウェアbaidu apolloの無料解説講座内容まとめ

自動運転 Robot

はじめに

こんにちは．ササキ(@saitosasaki)です．
今回はUdacityにあるbaiduの自動運転ソフトウェアapolloの無料解説講座を受講したので内容をまとめました．自分の気になったとこメインでまとめているので．すこし内容に偏りがあります（汗． www.udacity.com
この講座は文字通り"apolloの特徴"について各機能モジュール毎に簡単に説明して，プログラミング課題は無いです。倍速なら数時間で見れて，apolloの概要が掴めてとても良かったです．数式による説明もないので，「自動運転or自律移動ロボットなんもわからん」という人も見れると思います．

まとめ

注意：LはLessonの略です．

L1. 講座概要

"自動運転とは何か"から"apolloとは何か"までザックリ説明しています．
apollo structure
f:id:ssk0109:20190611150359p:plain

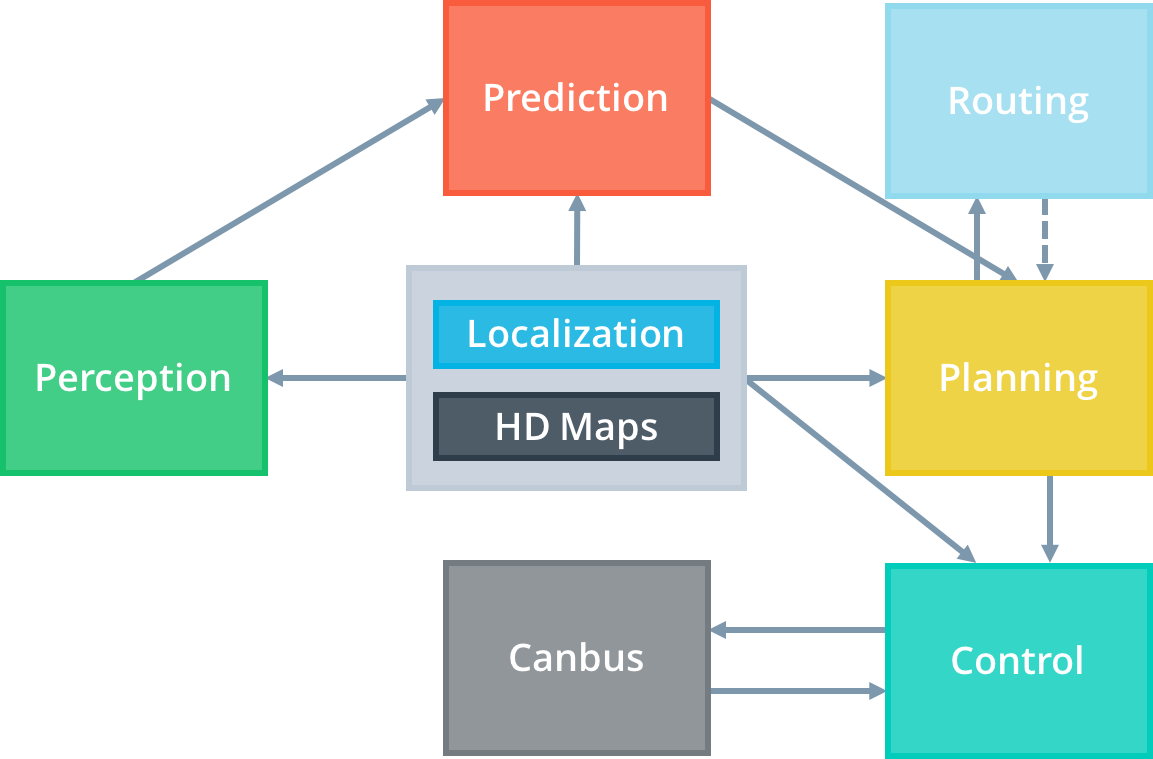
L2. HD(High Definition) Maps

自動運転にはgoogle mapのような地図ではなく三次元の高精度な地図が必要で，その説明をしています．

L3. Localization

自動運転におけるLocalizationの基本であるRTK-GNSS,INS,LiDAR Localization,Visual Localizationの説明をしています．
apolloではGNSS/INS/LiDARを複合をした自己位置推定を使用しており，それに関する論文がICRA2018で採択されています．

arxiv.org

L4. Perception

ニューラルネット，畳み込みニューラルネットを簡単に説明し，Perceptionにおいてはディープラーニングで物体検出，分類，セグメンテーションを使っていると説明しています．

L5. Prediction

ここでいうPredictionは自車両以外の物体の動きを予測することです．
予測にはモデルベースなものと機械学習によるデータドリブンなものがあります．
モデルベースな手法はLane Seqence-based Predictionと呼ばれるものを使っています．道路を複数のセグメントに分割し，動きのパターンをレーンセグメントのシーケンスとして記述します．
レーグセングメントの例（水色で囲まれているのがひとつのセグメントです．) f:id:ssk0109:20190611140159p:plain 機械学習による手法はターゲットのレーン予測にRNN(Recurrent Neuaral Network）を使っています．

L6. Plannning

経路計画はグロバールプランナーはA*，ローカルプランナーは経路-速度のDecopled Planning，Lattice Plannningが使われています．（余談ですが，ここだけ動画数が多くて気合が入ってる気がします．）

Frenet Coordinates
一般的な座標であるCartesian Coordinatesは車両にとって最適ではないので，Frenet Coordinates と呼ばれる道路に対して自動車の位置を表す座標系を使っています．
Cartesian Coordinates

Frenet Coordinates
Decopled Planning
Decopled PlanningはPlanningをパス計画と速度計画の2段階に分割します．まずパス計画では、車両が走行できる経路である候補曲線を生成し，パスをコストでランク付けし、最もコストの低いパスを選択します。次に速度計画において、このパスに沿って移動する速度を決めます。

L7. Control

Controlは「進行方向にPID，ステアリングにLQR(Liner Quandac Reglater)」と「MPC(Model Predictive Control)」があると説明しています．

2019-05-11

【論文】Google Cartographerの論文【ICRA2016】

Robot SLAM 論文 Cartographer

はじめに

こんにちは．ササキ(@saitosasaki)です．
私は以前Google Cartographer(OSS中でおそらく一番性能の良いグラフベースSLAM）の論文を読んだことがあったので復習のため、~~(かつどこにも解説スライドや記事が上がってなさそうなので)~~、まとめをブログに挙げます。

Github
github.com 論文
Real-Time Loop Closure in 2D LIDAR SLAM

予備知識

下記の解説論文を読めば、Cartographerの基礎となるgraph-based slamのことがわかると思います。
移動ロボットの環境認識 —地図構築と自己位置推定 - J-Stage

論文

概要

背景と課題
LIDAR-SLAMは、間取り図を取得する効率的な方法である。地図をリアルタイムで生成して可視化することで、オペレータはキャプチャデータの品質とカバレッジを評価できる。携帯型キャプチャプラットフォームを構築するには、限られた計算リソースの下で動作する必要がある。
提案手法
本論文では、5 cmの解像度でリアルタイムマッピングとループクロージャを実現するアプローチを紹介する。リアルタイムなループクロージャを達成するために、制約としてスキャン対サブマップの一致を計算するための分岐限定(branch-and-bound)法を使用する。
実験
確立された技術と競合することを示すために、提案手法と他のよく知られたアプローチと比較する。

スライド

今回のまとめはスライド形式にしてみました（というか結構前に自分が作ったのを修正しただけなのですが）。 speakerdeck.com

おわりに

スライドでまとめると、論文の直訳ではなく、自分の言葉で書く必要があるので、作るとより理解できてる気がします。発表するにはもうちょいスライドの内容を間引く必要がありますね。あともっとオリジナルの図を入れてわかりやくしたいですね。反省。
実験結果はオーソドックスで特筆することも無さ気なので書いてません。書いたほうがいいんですかね？
表現にいろいろ怒られそうなところはありますが、そのうち直します。…たぶん。

参考にした資料

論文と実装で変更された点

ほんとは別記事で書きたいのですが，とりあえずここに書いときます．

コスト関数
実装におけるコスト関数．

google-cartographer.readthedocs.io

sparseという言葉の取り扱い
論文だとグラフがspaerseなのを押し出していて，プログラムの初期のpose graphのプログラム名をsparse_pose_graph としていました．しかし，下記のissueで「pose graphはsparseなグラフなんだからsparseなんてつけるのはpoorだ」と言われて，作成者の方は最初こそ抵抗したものの，結局プログラムや関数名からsparseという言葉は無くなっています．

github.com

目次

はじめに

カテゴリー

資料まとめ

Google Cartographer

確率ロボティクスの勉強

論文読み

ROS2

その他

宣伝

目次

はじめに

コード置き場

環境

問題1：rclcpp_register_node_pluginsコマンド

問題2：create_subscription関数

問題3：メッセージをpublishする際の警告

結果

宣伝

追記

目次

はじめに

State Lattice Plannerとは

アルゴリズムの流れ

1. 終端状態のサンプリングステップ(Sampling)

2. パス生成ステップ(Trajectory Generation)

2.1 初期パラメータ決定

2.2 パラメータ最適化

2.2.1 パス生成

2.2.2 閾値チェック

2.2.3 パラメータ調整

3. パス選択ステップ

参考にしたもの

目次

はじめに

まとめ

L1. 講座概要

L2. HD(High Definition) Maps

L3. Localization

L4. Perception

L5. Prediction

L6. Plannning

L7. Control

目次

はじめに

予備知識

論文

概要

スライド

おわりに

参考にした資料

論文と実装で変更された点